红黑树的前身:2-3树简介
红黑树是是一种平衡查找树,以前浏览过好几次资料,都没有搞明白这种数据结构是啥意思;甚至看了极客时间的教程都一脸懵逼。一次偶然的机会看到了网络上的2-3树教程,顿时觉得原来红黑树也可以很简单。
这篇教程就是 CSDN《史上最简单清晰的红黑树讲解》
红黑树是2-3树的近似,它将2-3树变形为二叉树,这样就既保持了2-3树的性质,又具有了二叉树的方便。2-3树可以进一步扩展为B树(或者说2-3树是B树的一种特定实现),B树可以进一步扩展为B+树,B+树可以进一步扩展为B*树。
B树是多叉平衡树,二叉树也是B树的一种。M阶B树的出度范围是[ceil(M/2)-1, M - 1],比如二叉树只能是1,2-3树是1和2, 5阶树是2到4。
B+树是为了外存索引提出的改进版B树,如果只有内存场景,B树更好。B+树的优势是可以通过磁盘页间关联进行范围查询;另一个和B树显著的差别是B+树的数据都在叶子上。进一步,如果非叶子节点间也有指针关联,就是B*树。
上面CSDN的文章介绍的2-3树插入稍微有点复杂,其实2-3树的插入就一个行为:插入到叶子节点上,如果超度了就向上移动中间值。
下面通过几个例子先简单看一下。
对于2-node,直接插入变成3-node
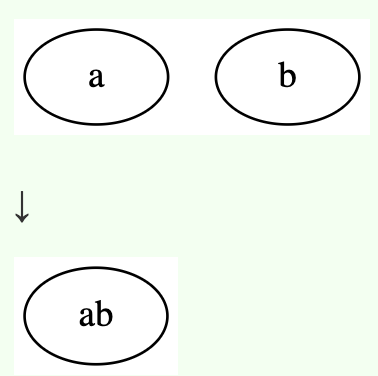
当把a插入到b结点上时插入到左边,当把b插入到a结点上时插入到右边。左小右大,需要比较一下,否则就不是查找树了。
画图工具由graphviz提供支持
对于3-node,先择位插入为4-node,然后分裂为3个2-node,并将中间节点上升
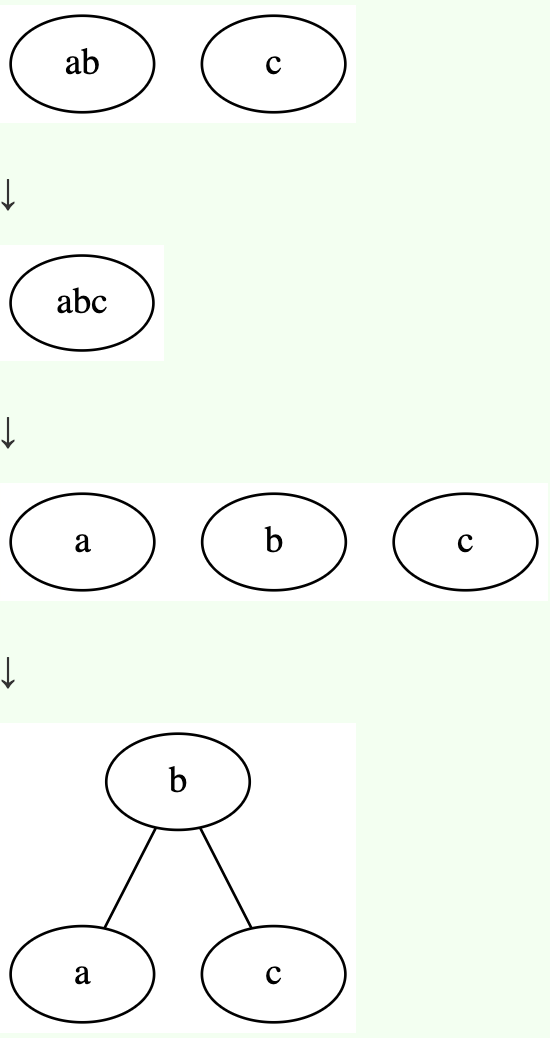
这样树的高度增加了。
插入一定发生在叶子节点
意思就是说,即使某个节点是2-node,插入不破坏树的规则,但是也不能直接插入到这里。
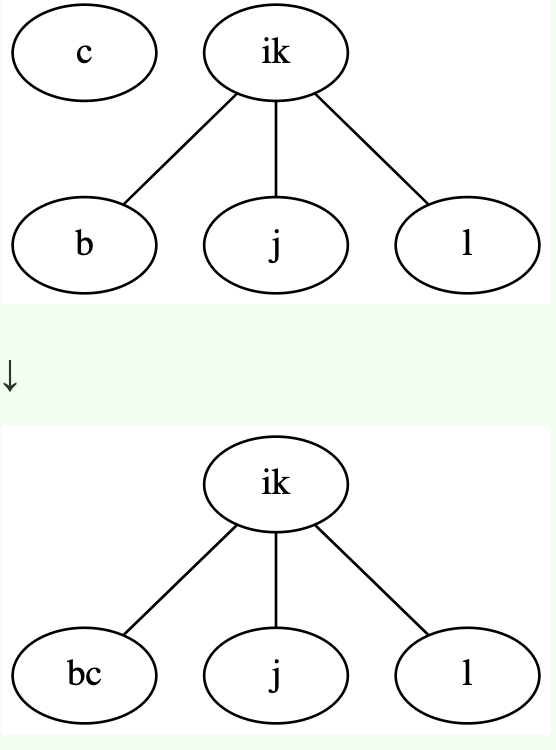
4-node分裂上升之后,如果上升的节点变成了4-node,要继续分裂
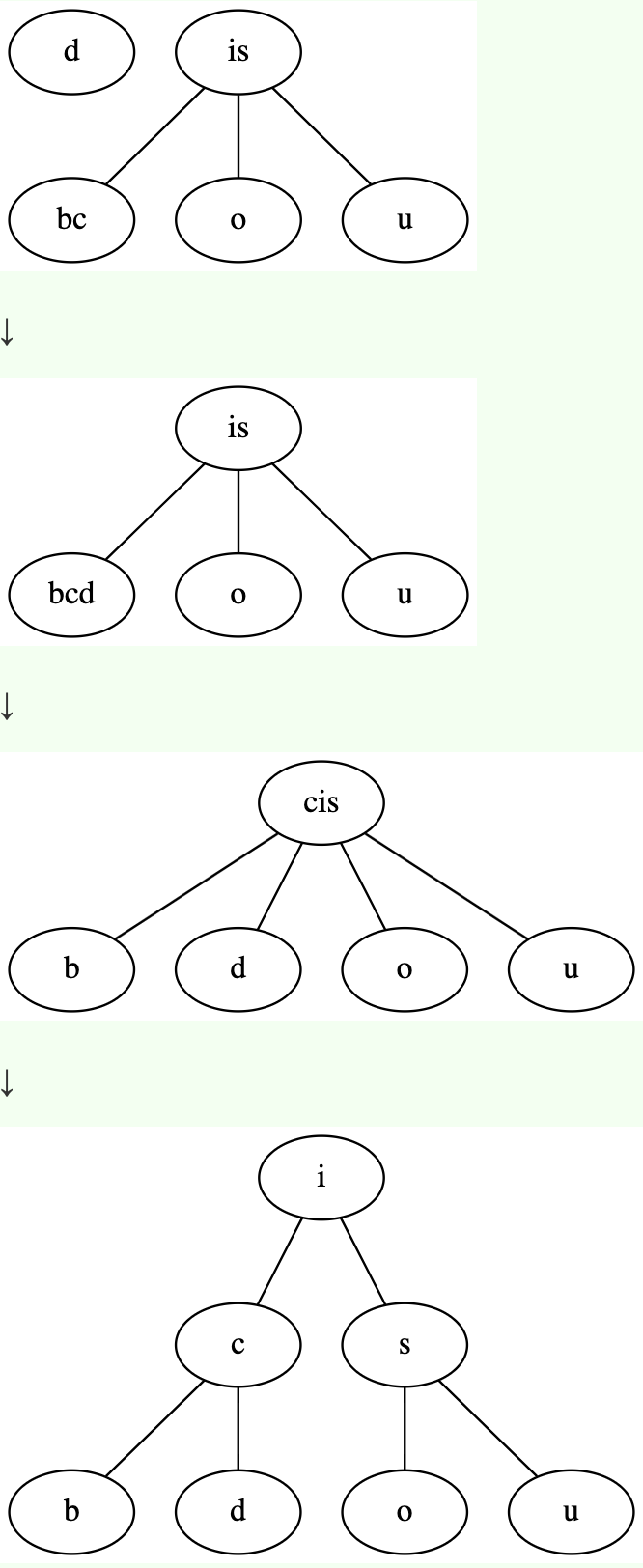
通过这几个例子大家应该也能大致了解2-3树的插入了。能不能动手实现一下呢?
因为前面提到的CSDN文章里面没有相应的代码,于是我打算花点时间写一下。结果我低估了2-3树的实现难度,用了一个下午竟然连插入都没有完全写好。
后来才知道,之前人们就是嫌2-3代码复杂才开始搞红黑树。也就是红黑树的代码都比2-3树简单,更别说泛化B树了
下面是我实现的2-3树插入的代码,这里我偷懒使用了Java已有的LinkedList数据结构,不过不影响对原理的理解:
import java.util.LinkedList;
import java.util.stream.Collectors;
public class TwoThreeTree<K extends Comparable<K>> {
private final LinkedList<K> keys;//节点key,最多3个元素
private final LinkedList<TwoThreeTree<K>> pointers;
private TwoThreeTree<K> parent;
public TwoThreeTree(K k, TwoThreeTree<K> parent) {
this.keys = new LinkedList<>();
this.pointers = new LinkedList<>();
keys.add(k);
this.parent = parent;
}
/**
* 打印当前节点和直系亲属
*
* @return 当前节点和直系亲属
*/
@Override
public String toString() {
return "TwoThreeTree{" +
keys +
"=>" + pointers.stream().map(j -> j.keys).collect(Collectors.toList()) +
'}';
}
public void printTree() {
TwoThreeTree<K> o = this;
while (o.parent != null) {
o = o.parent;
}
printTreeNode(o);
}
private void printTreeNode(TwoThreeTree<K> o) {
System.out.println(o);
if (!o.pointers.isEmpty()) {
o.pointers.forEach(this::printTreeNode);
}
}
public void entry(K k) {
TwoThreeTree<K> o = this;
while (o.parent != null) {
o = o.parent;
}
o.add(k);
}
private synchronized void add(K k) {
if (keys.size() == 1) {//2-node
if (keys.getFirst().equals(k)) {
return;
}
if (keys.getFirst().compareTo(k) > 0) {// to left
if (pointers.isEmpty()) {
keys.addFirst(k);// add as first key
} else {
pointers.getFirst().add(k); // proceed in left sub tree
}
} else { // to right
if (pointers.isEmpty() || pointers.size() == 1) {
keys.addLast(k);// add as last key
} else {
pointers.getLast().add(k); // proceed in right sub tree
}
}
} else if (keys.size() == 2) {//3-node
if (keys.getFirst().equals(k) || keys.getLast().equals(k)) {
return;
}
K first = keys.getFirst();
K second = keys.getLast();
if (first.compareTo(k) > 0) {// to left
if (pointers.isEmpty()) {
keys.addFirst(k);// have to change structure
promoteLeft();
} else {
pointers.getFirst().add(k);
}
} else if (second.compareTo(k) < 0) {// to right
if (pointers.isEmpty()) {
keys.addLast(k);// have to change structure
promoteRight();
} else {
pointers.getLast().add(k);
}
} else { // to middle
if (pointers.size() > 1) {
pointers.get(1).add(k);
} else {
keys.add(1, k);
promoteMiddle();
}
}
} else {
throw new RuntimeException("corrupted tree");
}
}
private void promoteMiddle() {
if (keys.size() < 3) {
return;
}
K first = keys.pollFirst();
K mid = keys.pollFirst();
K last = keys.getFirst();
if (first == null || last == null || mid == null) {
throw new RuntimeException("corrupted tree");
}
if (parent == null) {// the root
TwoThreeTree<K> newRoot = new TwoThreeTree<>(mid, null);
TwoThreeTree<K> newLeft = new TwoThreeTree<>(first, newRoot);
newRoot.pointers.add(newLeft);
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
newRoot.pointers.add(this);
this.parent = newRoot;
} else {
K pf = parent.keys.getFirst();
if (parent.keys.size() == 1) {
if (pf.compareTo(mid) > 0) { // from left sub
parent.keys.addFirst(mid);
TwoThreeTree<K> newLeft = new TwoThreeTree<>(first, parent);
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
parent.pointers.addFirst(newLeft);
parent.promoteLeft();// 递归处理
} else {
parent.keys.addLast(mid);
TwoThreeTree<K> newLeft = new TwoThreeTree<>(first, parent);
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
parent.pointers.add(1, newLeft);
parent.promoteRight();// 递归处理
}
} else {
K pl = parent.keys.getLast();
if (pf.compareTo(mid) > 0) { // from left sub
parent.keys.addFirst(mid);
TwoThreeTree<K> newLeft = new TwoThreeTree<>(first, parent);
parent.pointers.addFirst(newLeft);
parent.promoteLeft();// 递归处理
} else if (pl.compareTo(mid) < 0) {
parent.keys.addLast(mid);
TwoThreeTree<K> newRight = new TwoThreeTree<>(first, parent);
if (!pointers.isEmpty()) {
newRight.pointers.addLast(pointers.pollFirst());
newRight.pointers.getLast().parent = newRight;
}
if (!pointers.isEmpty()) {
newRight.pointers.addLast(pointers.pollFirst());
newRight.pointers.getLast().parent = newRight;
}
parent.pointers.add(2, newRight);
parent.promoteRight();// 递归处理
} else {
parent.keys.add(1, mid);
TwoThreeTree<K> newLeft = new TwoThreeTree<>(first, parent);
parent.pointers.add(1, newLeft);
parent.promoteMiddle();// 递归处理
}
}
}
}
/**
* 变成了4-node,需要自下而上变更
*/
private void promoteLeft() {
if (keys.size() < 3) {
return;
}
K first = keys.pollFirst(); // remove the first key
K mid = keys.pollFirst(); // remove the second key
if (first == null || mid == null) {
throw new RuntimeException("corrupted tree");
}
if (parent == null) {// the root
TwoThreeTree<K> newRoot = new TwoThreeTree<>(mid, null);
TwoThreeTree<K> newLeft = new TwoThreeTree<>(first, newRoot);
newRoot.pointers.add(newLeft);
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
newRoot.pointers.add(this);
this.parent = newRoot;
} else {
K pf = parent.keys.getFirst();
K ps = parent.keys.getLast();
if (pf.compareTo(mid) > 0) { // from left sub, always true
parent.keys.addFirst(mid);
TwoThreeTree<K> newLeft = new TwoThreeTree<>(first, parent);
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
parent.pointers.addFirst(newLeft);
parent.promoteLeft();// 递归处理
} else if (ps.compareTo(mid) < 0) {
parent.keys.addLast(mid);
TwoThreeTree<K> newLeft = new TwoThreeTree<>(first, parent);
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
if (!pointers.isEmpty()) {
newLeft.pointers.add(pointers.pollFirst());
newLeft.pointers.getFirst().parent = newLeft;
}
parent.pointers.add(1, newLeft);
parent.promoteRight();// 递归处理
} else {
parent.keys.add(1, mid);
TwoThreeTree<K> newLeft = new TwoThreeTree<>(first, parent);
parent.pointers.add(2, newLeft);
parent.promoteMiddle();// 递归处理
}
}
}
private void promoteRight() {
if (keys.size() < 3) {
return;
}
K second = keys.pollLast(); // remove the last one
K mid = keys.pollLast(); // remove the second key
if (second == null || mid == null) {
throw new RuntimeException("corrupted tree");
}
if (parent == null) {// the root
TwoThreeTree<K> newRoot = new TwoThreeTree<>(mid, null);
TwoThreeTree<K> newRight = new TwoThreeTree<>(second, newRoot);
newRoot.pointers.add(this);
this.parent = newRoot;
newRoot.pointers.add(newRight);
if (pointers.size() > 2) {
newRight.pointers.addLast(pointers.remove(2));
newRight.pointers.getLast().parent = newRight;
}
if (pointers.size() > 2) {
newRight.pointers.addLast(pointers.remove(2));
newRight.pointers.getLast().parent = newRight;
}
} else {
K pf = parent.keys.getFirst();
K ps = parent.keys.getLast();
if (pf.compareTo(mid) > 0) { // from left sub
parent.keys.addFirst(mid);
TwoThreeTree<K> newRight = new TwoThreeTree<>(second, parent);
if (pointers.size() > 2) {
newRight.pointers.addLast(pointers.remove(2));
newRight.pointers.getLast().parent = newRight;
}
if (pointers.size() > 2) {
newRight.pointers.addLast(pointers.remove(2));
newRight.pointers.getLast().parent = newRight;
}
parent.pointers.add(1, newRight);
parent.promoteLeft();// 递归处理
} else if (ps.compareTo(mid) < 0) {
parent.keys.addLast(mid);
// parent.promoteRight();
TwoThreeTree<K> newRight = new TwoThreeTree<>(second, parent);
if (pointers.size() > 2) {
newRight.pointers.addLast(pointers.remove(2));
newRight.pointers.getLast().parent = newRight;
}
if (pointers.size() > 2) {
newRight.pointers.addLast(pointers.remove(2));
newRight.pointers.getLast().parent = newRight;
}
parent.pointers.addLast(newRight);
parent.promoteRight();// 递归处理
} else {
parent.keys.add(1, mid);
TwoThreeTree<K> newRight = new TwoThreeTree<>(second, parent);
if (pointers.size() > 2) {
newRight.pointers.addLast(pointers.remove(2));
newRight.pointers.getLast().parent = newRight;
}
if (pointers.size() > 2) {
newRight.pointers.addLast(pointers.remove(2));
newRight.pointers.getLast().parent = newRight;
}
parent.pointers.add(2, newRight);
parent.promoteMiddle();// 递归处理
}
}
}
}
代码链接:https://github.com/davelet/two-three-tree-node/blob/master/TwoThreeTree.java
这是经过多个用例测试形成的实现,可能还有隐藏问题我没有发现。如果你发现了可以留言。
下面是我的测试用例:
public class TestCase {
public static void main(String[] args) {
test1();
System.out.println("======insertToLeft");
insertToLeft();
System.out.println("======insertToLeftMiddle");
insertToLeftMiddle();
System.out.println("======insertToMiddle");
insertToMiddle();
System.out.println("======insertToMidMiddle");
insertToMidMiddle();
System.out.println("======insertToMidRight");
insertToMidRight();
System.out.println("======insertToRight");
insertToRight();
System.out.println("======insertToRightLeft");
insertToRightLeft();
System.out.println("======insertToRightMiddle");
insertToRightMiddle();
System.out.println("======insertToRightUpper");
insertToRightUpper();
System.out.println("======insertToRightUpper2");
insertToLeftUpper2();
System.out.println("======insertToRightUpper3");
insertToLeftUpper3();
System.out.println("======insertToRightUpper4");
insertToLeftUpper4();
System.out.println("======insertToRightUpper4");
insertToRightUpper2();
System.out.println("======insertToRightUpper4");
insertToRightUpper4();
}
private static void test1() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(190, null);
tree.entry(200);
tree.entry(50);
tree.entry(100);
tree.entry(191);
tree.entry(192);
tree.entry(6);
tree.entry(7);
tree.printTree();
}
private static void insertToLeft() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(100);
tree.entry(30);//left
tree.printTree();
}
private static void insertToLeftMiddle() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(100);
tree.entry(60);//middle
tree.printTree();
}
private static void insertToMiddle() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(100);
tree.entry(150);//middle
tree.printTree();
}
private static void insertToMidMiddle() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(100);
tree.entry(150);//middle
tree.entry(180);
tree.entry(160);//middle
tree.printTree();
}
private static void insertToMidRight() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(100);
tree.entry(150);//middle
tree.entry(160);
tree.entry(180);//right
tree.printTree();
}
private static void insertToRight() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(100);
tree.entry(150);
tree.entry(160);
tree.entry(280);
tree.entry(380);//right
tree.printTree();
}
private static void insertToRightLeft() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(100);
tree.entry(150);
tree.entry(160);
tree.entry(280);
tree.entry(380);//right
tree.entry(370);//left
tree.printTree();
}
private static void insertToRightMiddle() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(100);
tree.entry(150);
tree.entry(160);
tree.entry(280);
tree.entry(380);//right
tree.entry(370);//left
tree.entry(375);//middle
tree.printTree();
}
private static void insertToRightUpper() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(100);
tree.entry(150);
tree.entry(160);
tree.entry(280);
tree.entry(380);//right
tree.entry(370);//left
tree.entry(375);
tree.entry(372);
tree.entry(373);
tree.printTree();
}
private static void insertToLeftUpper2() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(60);
tree.entry(220);
tree.entry(280);
tree.entry(350);
tree.entry(380);
tree.entry(70);
tree.entry(370);
tree.entry(320);
tree.entry(58);
tree.entry(55);
tree.printTree();
}
private static void insertToLeftUpper3() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(60);
tree.entry(220);
tree.entry(280);
tree.entry(350);
tree.entry(380);
tree.entry(70);
tree.entry(370);
tree.entry(320);
tree.entry(58);
tree.entry(62);
tree.entry(63);
tree.printTree();
}
private static void insertToLeftUpper4() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(60);
tree.entry(220);
tree.entry(280);
tree.entry(350);
tree.entry(380);
tree.entry(70);
tree.entry(370);
tree.entry(320);
tree.entry(58);
tree.entry(210);
tree.entry(215);
tree.printTree();
}
private static void insertToRightUpper2() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(60);
tree.entry(220);
tree.entry(280);
tree.entry(350);
tree.entry(380);
tree.entry(70);
tree.entry(370);
tree.entry(320);
tree.entry(58);
tree.entry(210);
tree.entry(215);
tree.entry(360);
tree.printTree();
}
private static void insertToRightUpper4() {
TwoThreeTree<Integer> tree = new TwoThreeTree<>(200, null);
tree.entry(300);
tree.entry(50);
tree.entry(60);
tree.entry(220);
tree.entry(280);
tree.entry(350);
tree.entry(380);
tree.entry(70);
tree.entry(370);
tree.entry(320);
tree.entry(58);
tree.entry(210);
tree.entry(215);
tree.entry(360);
tree.entry(368);
tree.entry(365);
tree.printTree();
}
}
红黑树
2-3树的插入说完了,这里说一下和红黑树的区别。
红黑树是2-3树的变形,它将2-3树中的3-node变为2个2-node:
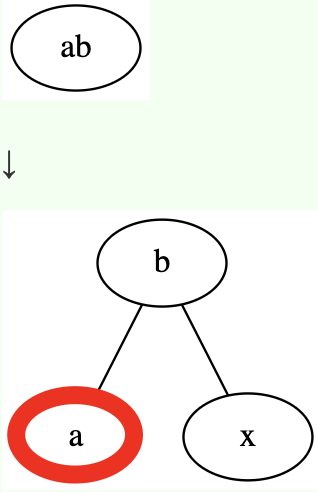
将3-node中的第一个元素做为第二个元素的左孩子,并且将其染红:这些节点就是红节点,其他节点都是黑节点 —— 所以叫红黑树。
通过红节点出来的过程可以看出来,红节点是不会相邻的,因为3-node转为红黑树节点后第二个元素是黑节点。
