一些无字证明

发表于2020-06-28，长度1076， 172个单词， 3分钟读完

这是网络上收集到的一些数学上的无字证明。非常有意思，放在这里简单解释一下。当然也为了自己后面更深刻的记忆。

奇数和公式

从1开始的连续奇自然数的和大家比较熟悉，这个也比较简单，就是一个等差数列：

\[1+3+5+\cdots + (2n-1) = n^2\]

以前我们的记忆方式是“首尾相加，乘高除以2”。它的证明方式可如下：

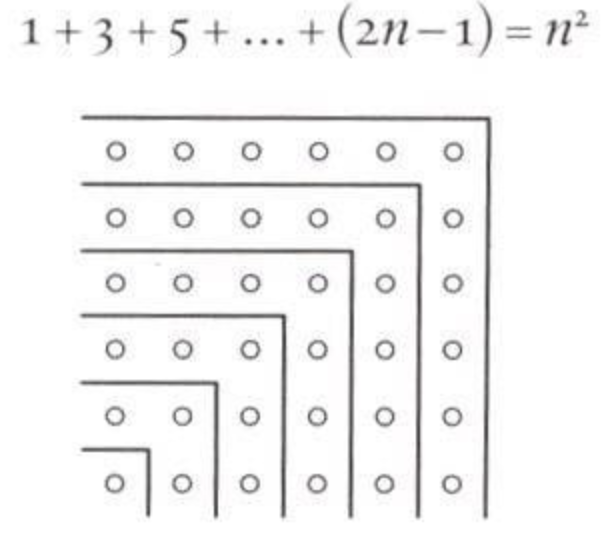
连续奇数个物体以拐角方式摆放，显然最终会形成一个方阵。

1/4等比数列之和

首项和公比都是 \(\frac{1}{4}\) 的数列之和我们可以用等比数列公式（首项除以公差对1的补）直接得出结果：

\[\sum_1^\infty \frac{1}{4^n} = \frac{1}{4}+ \frac{1}{16}+ \frac{1}{64} + \cdots = \frac{1}{3}\]

它的简洁证明如下：

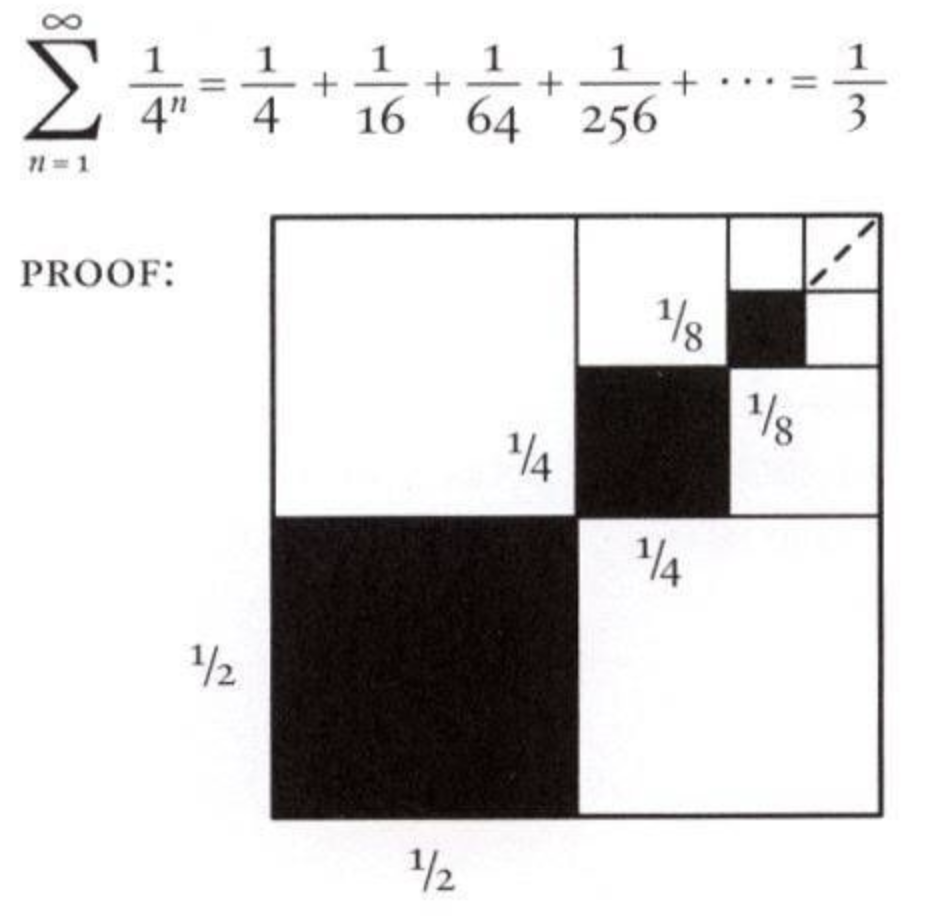
如果你打算惊呼一声，那我觉得你更应该惊呼下面这个等价证明：

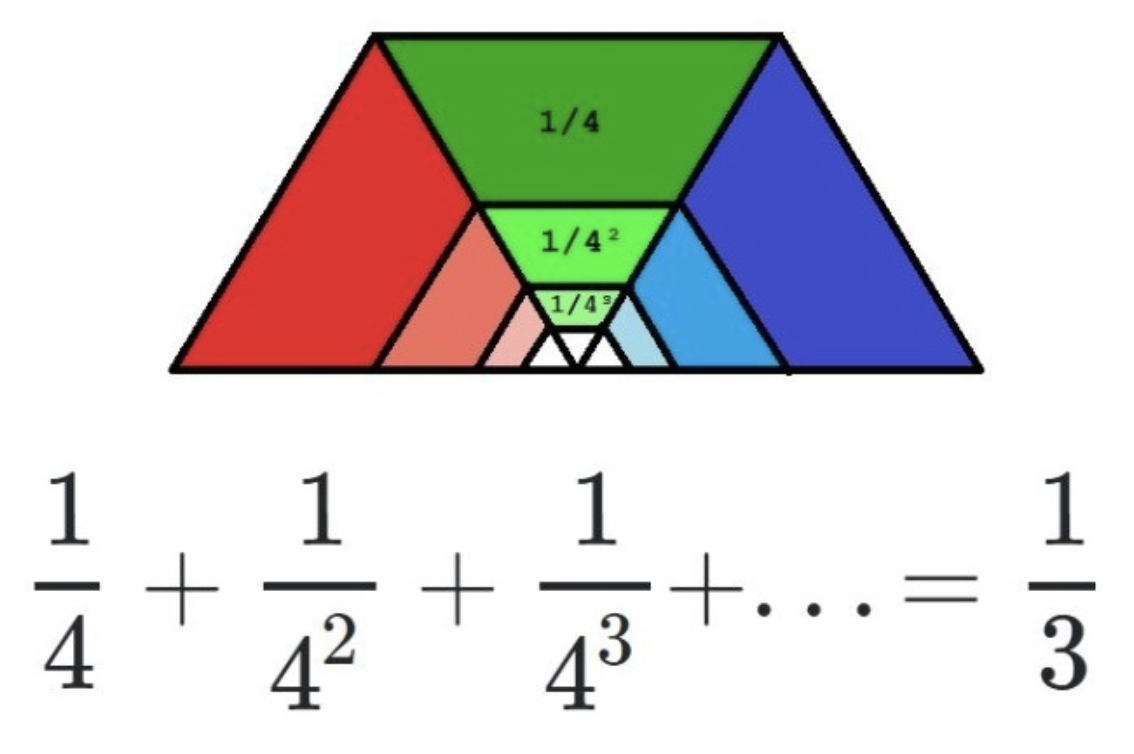
这个是啥意思呢？明白第一个（就是最大的）1/4就容易理解了。图中标出了1/4，为什么它是1/4呢？

还有一个与之类似的证明：

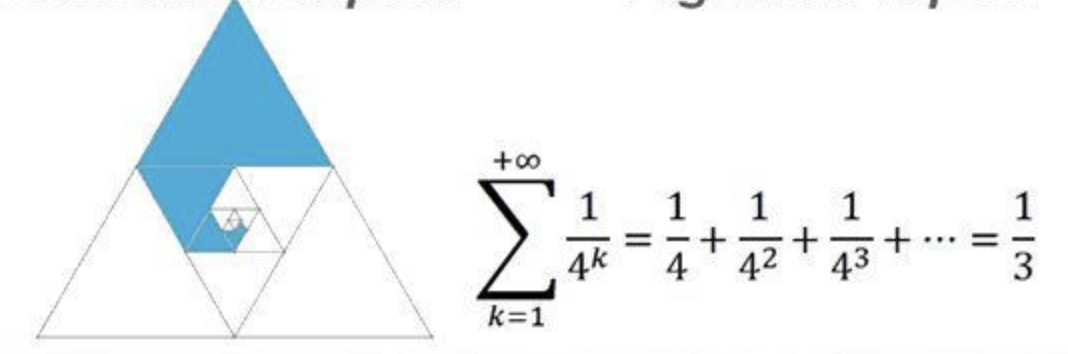
自然数平方和的3倍

\[3(1^2+2^2+3^2+\cdots + n^2) = (2n+1)(1+2+\cdots + n)\]

这个公式我是第一次见到。它的无字证明有些神奇：

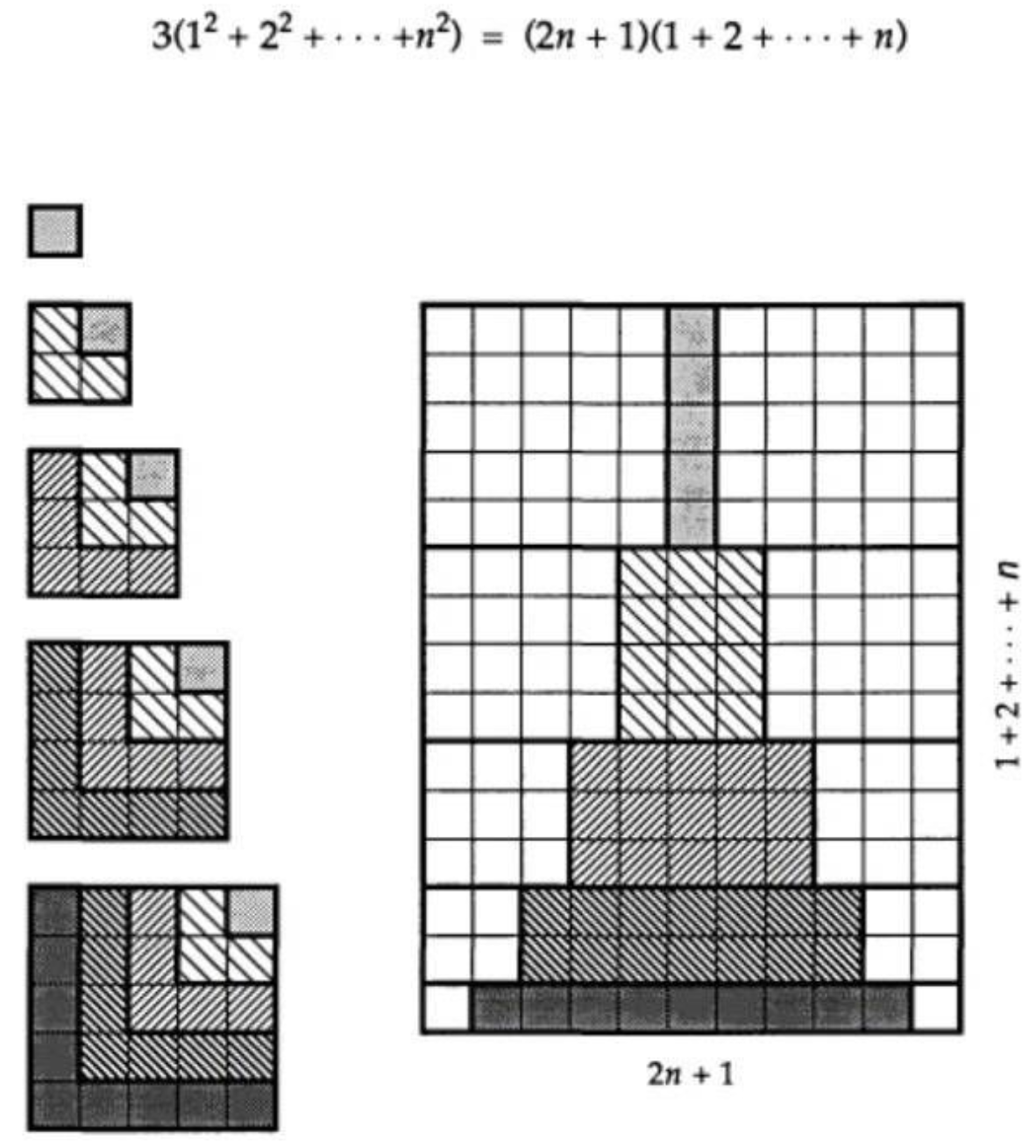
把每个方阵像奇数和证明的方式一样拐角分层，把同一层的都放一起，最终会形成上图中的阴影部分（中间部分）。这个阴影的下底宽是 \(2n-1\) ，高度是 \((1+2+\cdots + n)\) 。然后看图中阴影以外的部分，左右都一样，面积相等，它们都是连续奇数方阵的倒置。最终拼成的大图是个矩形，面积就是 \((2n+1)(1+2+\cdots + n)\)

三变量根号不等式

\[\sqrt{a^2+b^2} + \sqrt{b^2+c^2} + \sqrt{c^2+a^2} \ge \sqrt{2}(a+b+c)\]

这个不等式的证明比较容易理解也：

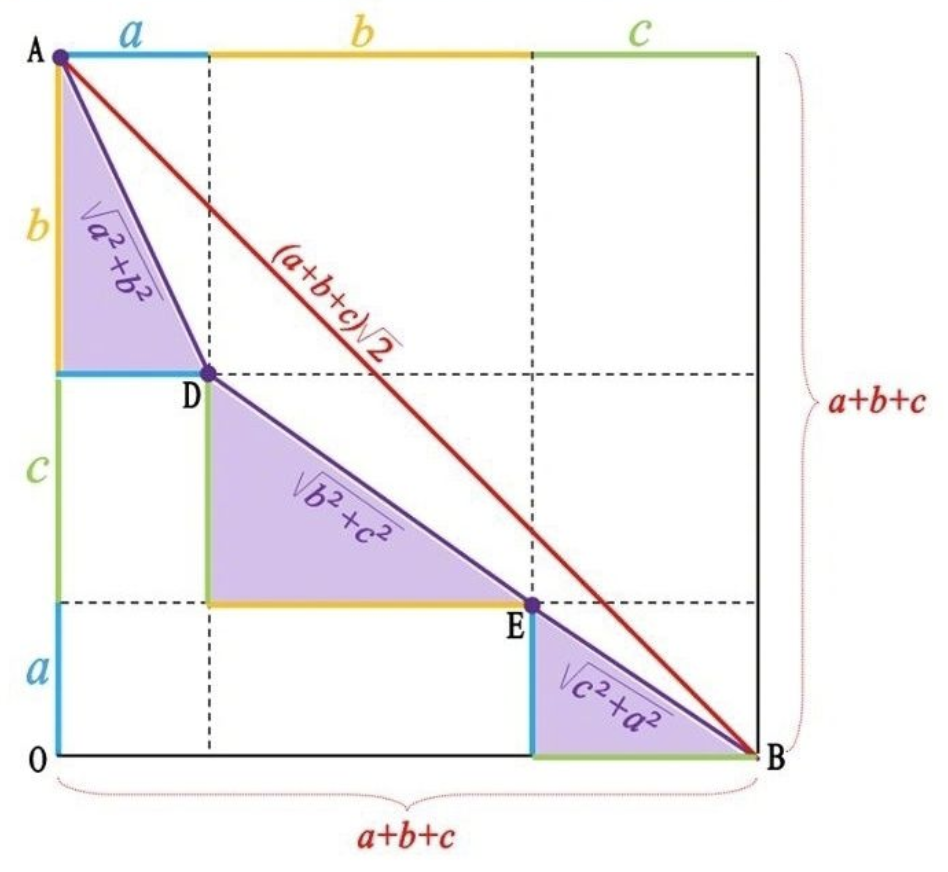
立方差公式

立方差大家应该比较熟悉：

\[a^3-b^3 = (a-b)(a^2+ab+b^2)\]

它的证明非常简单，小学生都能看懂：

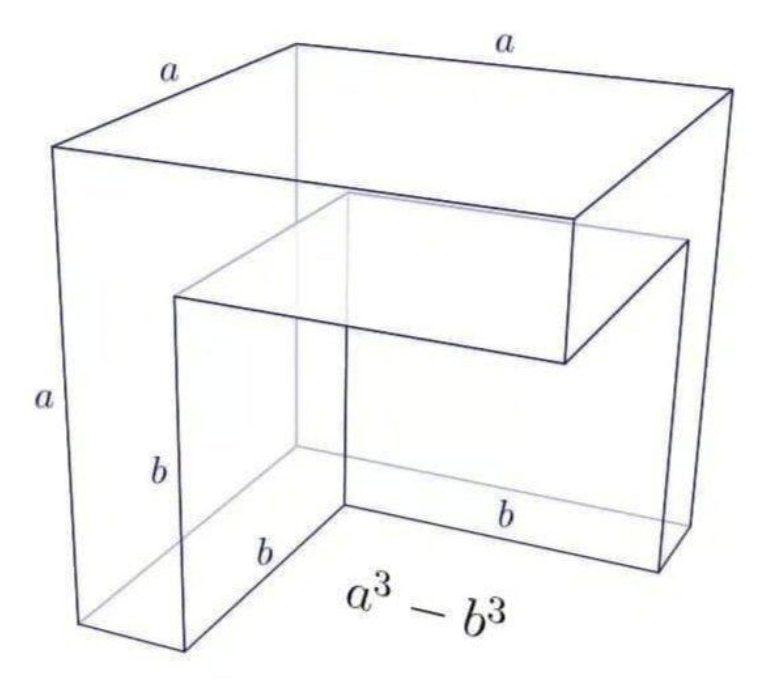
把这个不规则图像切成三个立方体即可：

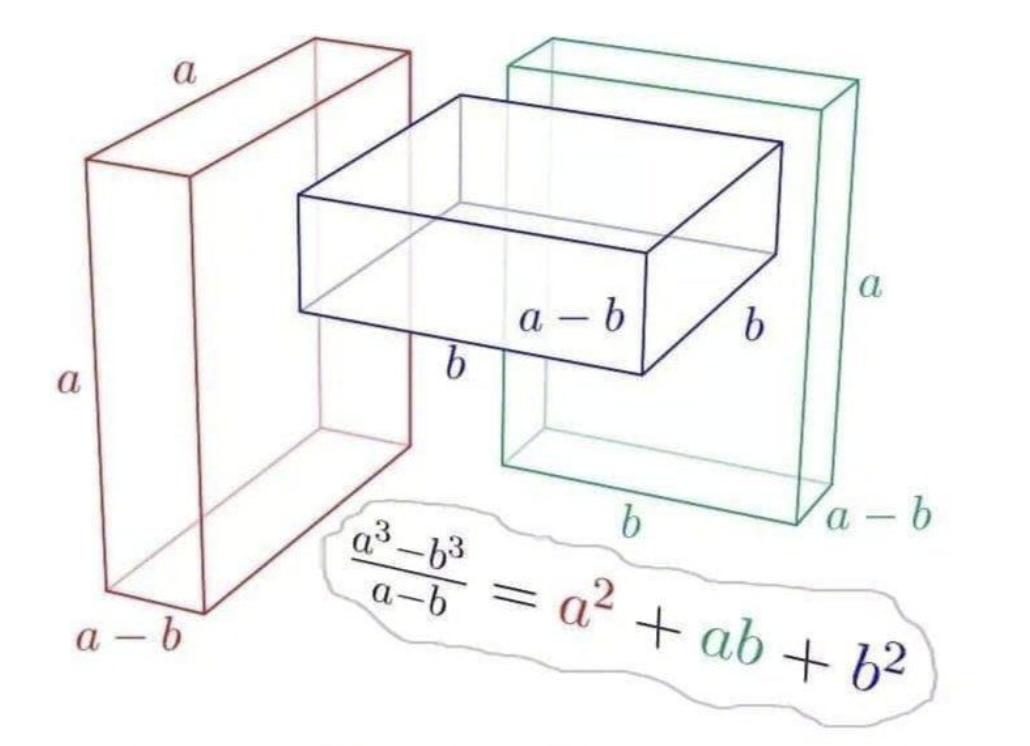
立方和公式

立方和也比较出名：

\[1^3+2^3+3^3+\cdots + n^3 = (1+2+3+\cdots+n)^2\]

它的证明应该也都能看懂：

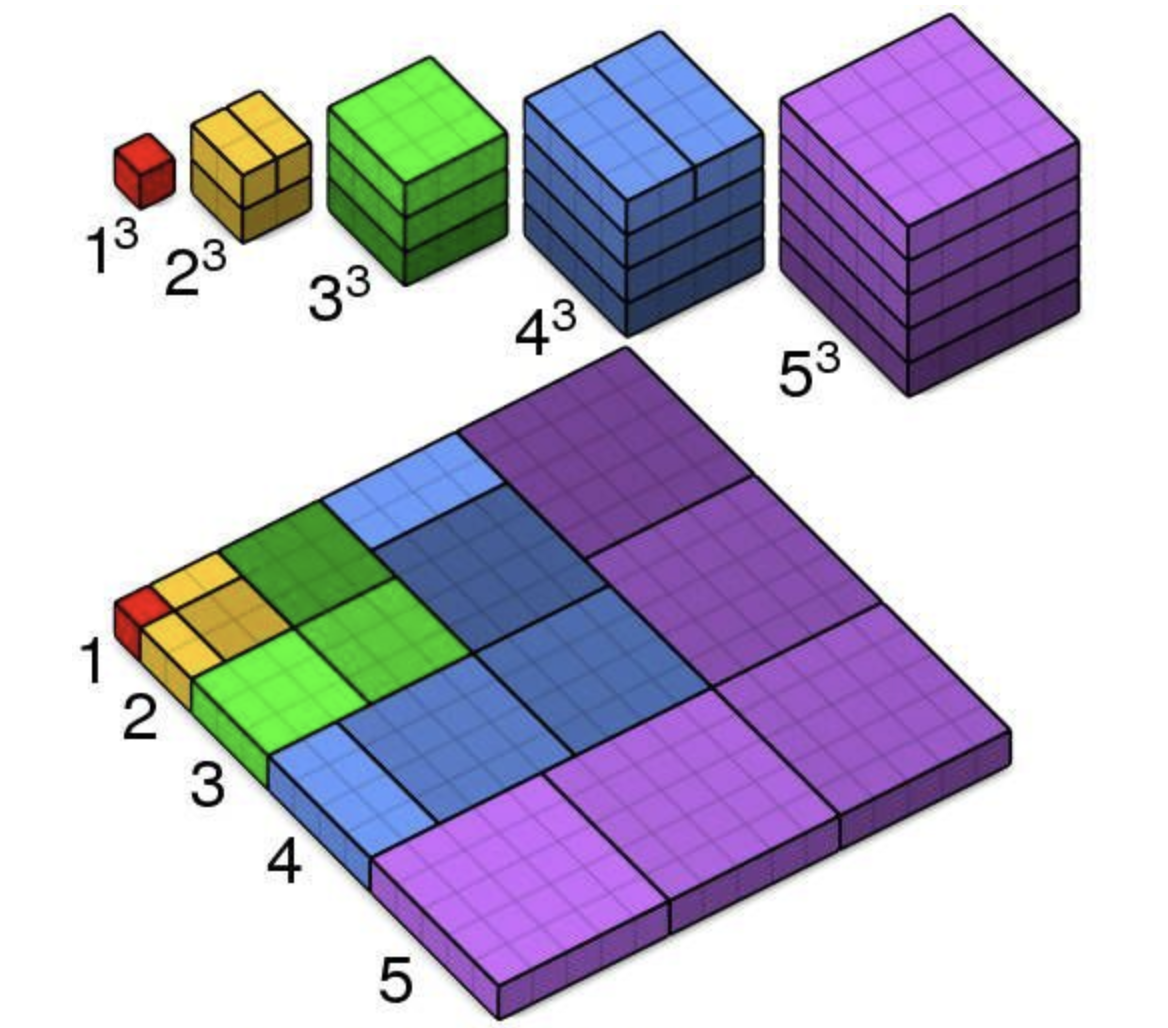
只有一点需要注意就是，奇数项和偶数项的拆分规则不一样。

三角函数

下面是三个三角函数的和角或倍角公式，都比较简单，就不细说了。

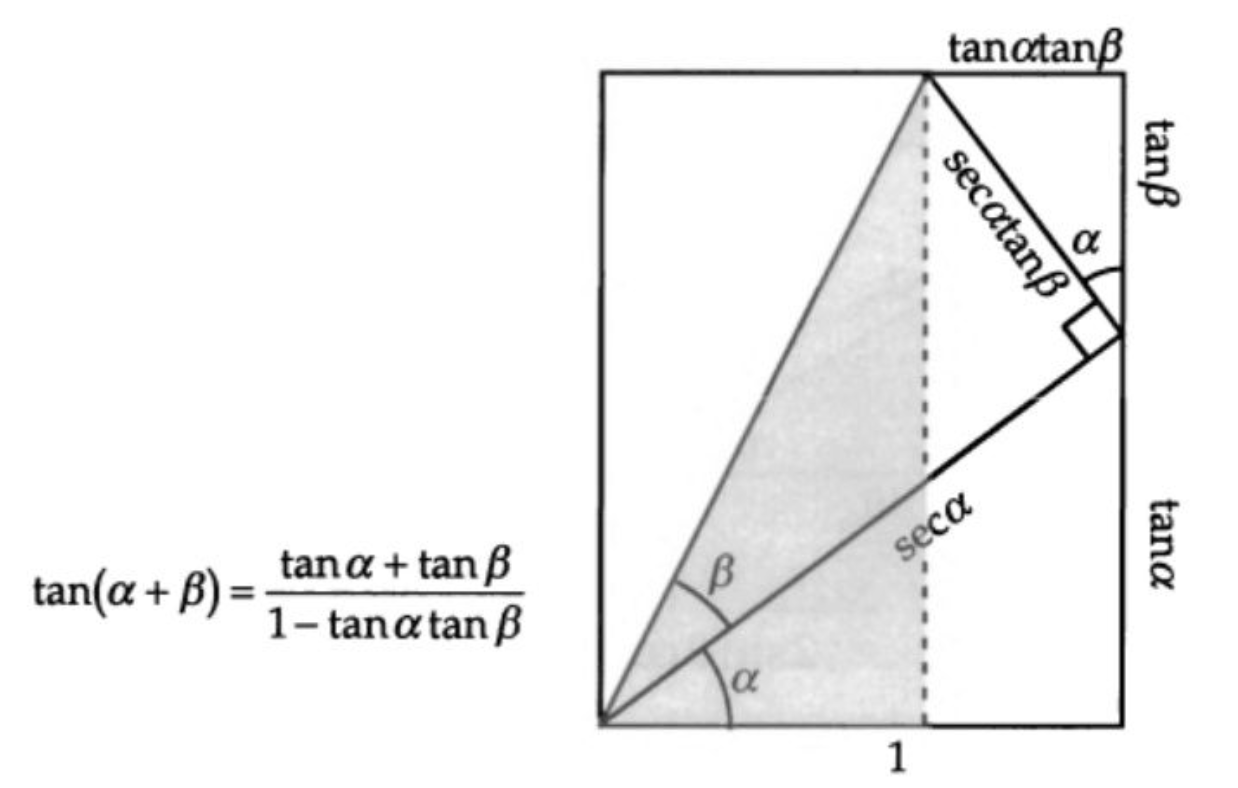
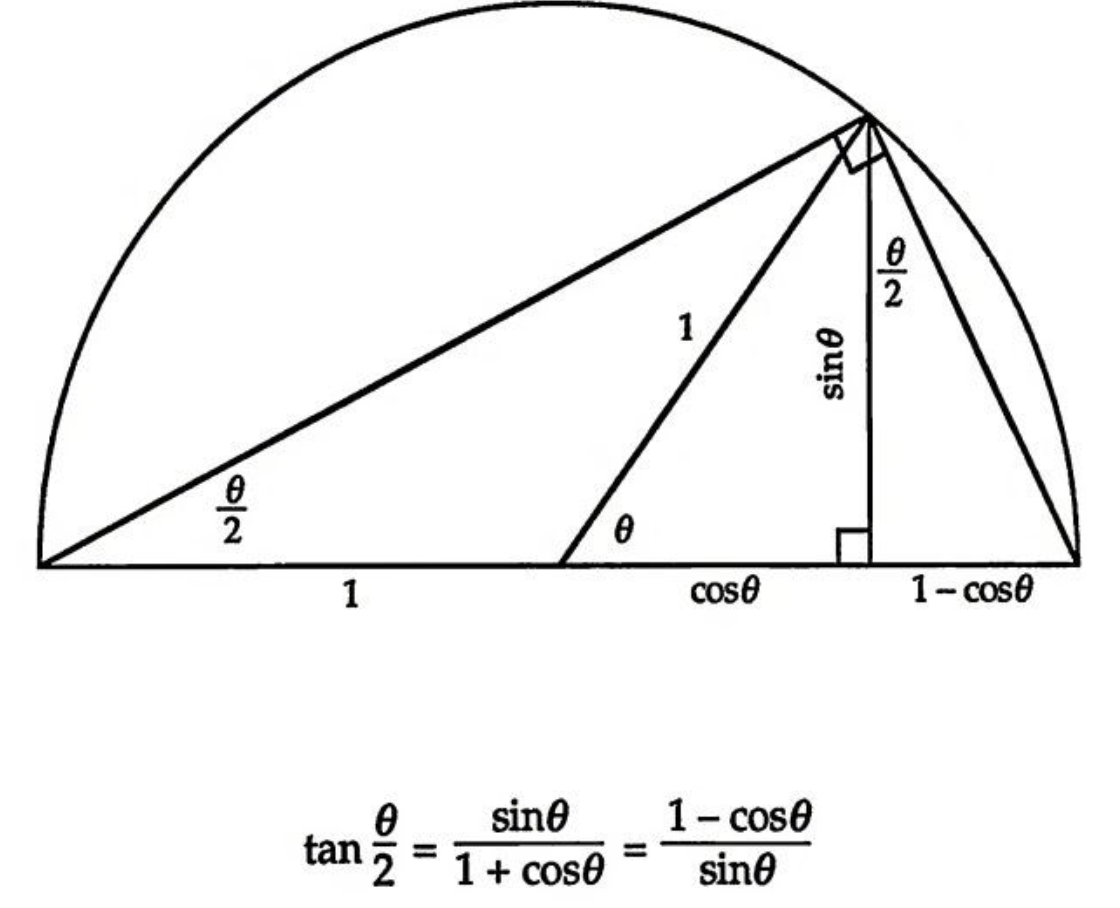
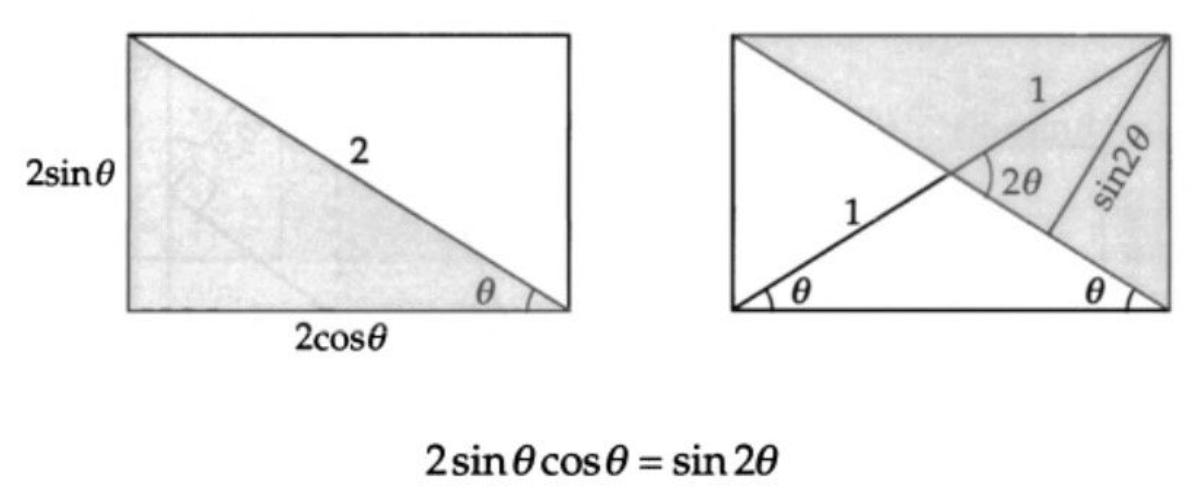
儿歌：狼打柴，狗烧火，小猫在炕上捏馍馍；馍馍呢？狗吃了！狗呢？钻洞了！洞呢？雪埋了！血呢？化水了！水呢？

Written on June 28, 2020

分类： blog，标签： math

如果你喜欢，请赞赏！ davelet

davelet