素数定理简史(三)
黎曼是狄利克雷的弟子,他的博士生导师是高斯,他在自己的文章中表达过过对高斯和狄利克雷比较推崇。
高斯于1855年离世,4年后狄利克雷去世。两位最尊敬的老师在这么短时间内先后去世,不得不说黎曼是受到严重打击的。而在这4年间,黎曼的父母、姐妹、老婆也都先后去世,更让黎曼觉得世事孤独。1866年(狄利克雷去世7年后)黎曼离世时还不到40岁。
黎曼级数也是p级数,只不过由于习惯,大家常把自变量使用s表示: \(\zeta(s) = \sum n^{-s}\)
前面也知道,当s大于1时级数收敛。下面是前几个级数和:
| N | 前12位级数和 |
|---|---|
| 1 | 发散 |
| 2 | 1.644934066848 |
| 3 | 1.202056903159 |
| 4 | 1.082323233711 |
| 5 | 1.036927755143 |
| 6 | 1.017343061984 |
黎曼主要考虑的自变量连续的情况,而不是前面我们看到的几个离散整数值。当s>1时,黎曼函数的图像有点像第一象限的反比例函数:自变量越大,值无限接近1;自变量从右侧接近1,值会无限大。
其他区域呢?当s=1时就是调和级数,发散;当s=0呢,是所有项都是1,明显也发散。s=1/2时,是所有自然数算术平方根的倒数和: \(\zeta(\frac{1}{2})=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots>1+\frac{1}{2}+\frac{1}{3}+\cdots\) 所以也发散。负数呢?比如-1: \(\zeta(-1)=1+2+3+\cdot\) 全体自然数的和,也发散。
可能有人会说:全体自然数的和哪里发散了,不是-1/12吗 o(╥﹏╥)o
可能还有人说:黎曼函数的定义域不是0到1吗,为什么反而大于1的时候有值,小于1没有值呢…
欧拉积公式
现在我们对黎曼函数做一些处理:从第一个素数2开始,给黎曼函数两边乘以以素数做底、自变量做指数的倒数:
\[\frac{1}{2^s}\zeta(s)=\frac{1}{2^s}+\frac{1}{4^s} + \frac{1}{6^s}+\cdots\]得到了原式中的全部偶数项。现在用原式减去它得到全部奇数项:
\[\zeta(s) - \frac{1}{2^s}\zeta(s) \\=\underline{ (1-\frac{1}{2^s})\zeta(s)= 1+ \frac{1}{3^s}+\frac{1}{5^s} + \frac{1}{7^s}+\cdots }\]接下来使用第二个素数3的指数去乘上式(刚才用的2的指数):
\[\frac{1}{3^s}(1-\frac{1}{2^s})\zeta(s)= \frac{1}{3^s}+\frac{1}{9^s} + \frac{1}{15^s}+ \frac{1}{21^s}+\cdots\]继续用原式减去这个结果,得到所有不是2或3的倍数的项:
\[(1-\frac{1}{2^s})\zeta(s)-\frac{1}{3^s}(1-\frac{1}{2^s})\zeta(s)\\= \underline{ (1-\frac{1}{3^s})(1-\frac{1}{2^s})\zeta(s) =1+\frac{1}{5^s}+\frac{1}{7^s}+\frac{1}{11^s} + \frac{1}{13^s}+\frac{1}{17^s}+\cdots }\]接下来用同样的方法把5的倍数的项也去掉,两边都乘5的指数:
\[\frac{1}{5^s}(1-\frac{1}{3^s})(1-\frac{1}{2^s})\zeta(s)= \frac{1}{5^s}+\frac{1}{35^s}+\frac{1}{55^s} + \frac{1}{65^s}+\frac{1}{85^s}+\cdots\]上下相减,得到所有不是2、3、5的倍数的项:
\[\underline{ (1-\frac{1}{5^s})(1-\frac{1}{3^s})(1-\frac{1}{2^s})\zeta(s)= 1+\frac{1}{7^s}+\frac{1}{11^s} + \frac{1}{13^s}+\frac{1}{17^s}+\cdots }\]大家已经应该能非常清晰的看明白这个过程了:就是用埃拉托色尼筛法把前面任意项素数干掉。比如我们一直处理到素数997:
\[(1-\frac{1}{997^s})(1-\frac{1}{991^s})\cdots(1-\frac{1}{5^s})(1-\frac{1}{3^s})(1-\frac{1}{2^s})\zeta(s)\\= 1+\frac{1}{1009^s}+\frac{1}{1013^s} + \frac{1}{1019^s}+\frac{1}{1021^s}+\cdots\]如果自变量s是大于1的,那上式的值就是略大于1的一个数。比如s=3时值是1.00000006731036081534…所以是不是有可能当上面筛的过程足够长(无限长)就能得到
\[\cdots(1-\frac{1}{11^s})(1-\frac{1}{7^s})(1-\frac{1}{5^s})(1-\frac{1}{3^s})(1-\frac{1}{2^s})\zeta(s)=1\]因为左边每乘一项,右边就少一项(实际少的是一个素数和一些合数),一直搞下去右边1以外的项都到左边了。
现在把左边黎曼函数的系数移项到右边:
\[\zeta(s)=\frac{1}{1-\frac{1}{2^s}}\times\frac{1}{1-\frac{1}{3^s}}\times\frac{1}{1-\frac{1}{5^s}}\times\frac{1}{1-\frac{1}{7^s}}\times\frac{1}{1-\frac{1}{11^s}}\times \cdots\]也就是说,我们有:
\[\sum n^{-s} =\prod_p (1-p^{-s})^{-1}\]其中,n是全体自然数,p是全体素数。
上面这个式子也说明了素数有无穷多个,因为如果素数有限,那么右面就是个能够算出来的值;但是左边有可能是调和级数会发散的
上面这个将全体正整数和转换为全体素数积的式子就是“欧拉积公式”。
改进版素数定理:对数积分公式
要继续研究素数定理,这里需要引入一个新的函数: \(\ln ^ {-1} t\) 的积分:
\[\int_{0}^{x} \frac{1}{\ln t} dt\]这个积分不能使用我们已知的其他普通函数表达,所以数学家为了方便,将它命名成
\[Li(x)\]这个函数就是对数积分函数。它的定义域是除1外的所有正数,图像如下(横轴被拉长了,所以图像有点矮,在1.451369…处值为0):
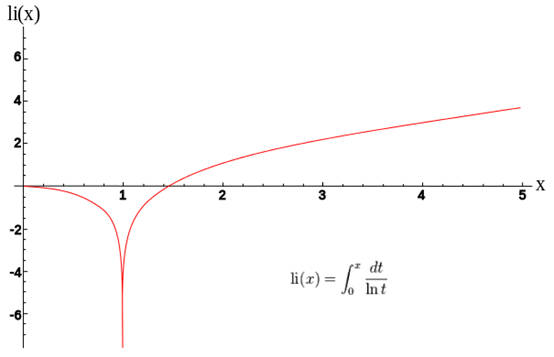
为什么Li(x)重要呢?因为它是比前面我们说的N/ln N对π(x)更好的估计。所以这里重新表述一下素数定理:
改进版PNT: π(x)趋近于Li(x)
另外对于所有的x, \(Li(x) > \pi(x) > \frac{x}{\ln x}\)
